Question

ASAP NEED HELP DUE TMR!!!

Answer 1

a = 6, b = -36

Explanation:

We have to convert the expression in the form of a perfect square. Therefore, we have to find another number when added with x² + 12x, can be converted to the perfect square.

So, we rewrite:

`\displaystyle{(x^2+12x+n)-n}`

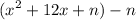
Where n is the number that can make the expression become a perfect square. We also subtract with n or else the equation will not equal the original equation.

To find n that makes the expression a perfect square, we can apply the formula:

`\displaystyle{n =\left( (b)/(2) \right)^2}`

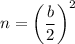
Substitute b = 12:

`\displaystyle{n =\left( (12)/(2) \right)^2}\\\\\displaystyle{n =36}`

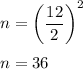
Hence:

`\displaystyle{(x^2+12x+n)-n = (x^2+12x+36)-36}\\\\\displaystyle{ (x^2+12x+36)-36 = (x+6)^2-36}`

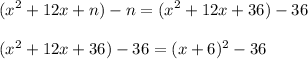
Therefore, the form can be rewritten in:

`\displaystyle{x^2+12x = \left(x+6\right)^2 -3 6}`

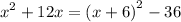
When comparing two equations, we can conclude that a = 6 and b = -36