Question

Please help asap!! <3

One interval is given in interval notation, another in set-builder notation. Match the equivalent intervals.

Answer 1

In order:

`\displaystyle{1.) \ \{ x \ | \ x \in \mathbb{R} \}} \\\\ \displaystyle{2.) \ \ x \ } \\\\ \displaystyle{3.) \ \ x \ } \\\\ \displaystyle{4.) \ \ \ -\infty < x < 3 \}`

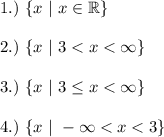
Explanation:

1.) To explain this answer, the interval notation gives that the interval is between -∞ to ∞. This means that x-values can be anything in the set of all real numbers. Hence, we write in the set builder notation as shown.

2.) Kindly remember that in the interval notation, the round bracket ( ) represents the open interval. An open interval is an interval that does not include the number itself. For example, (3, 4) in interval notation means any numbers between 3 and 4, not within 3 and 4. Hence, we can rewrite (3, 4) as 3 < x < 4. The same applies to the second answer.

3.) Same as the second but in front of 3, there's a square bracket. A square bracket represents the closed interval which means that it includes that number too. Hence, [3, ∞) means that any number ranging from 3 to a never-ending number. We can rewrite it as 3 ≤ x < ∞.

4.) The same explanation as number 2.