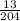Question

two cards are drawn without replacement from a standard deck of 52 playing cards what is the probability of choosing a club and then without replacement a spade

Answer 1

occurringGiven a total of 52 playing cards, comprising of Club, Spade, Heart, and Spade.

`\begin{gathered} n(\text{club) = 13} \\ n(\text{spade) =13} \\ n(\text{Heart) = 13} \\ n(Diamond)=\text{ 13} \\ \text{Total = 52} \end{gathered}`

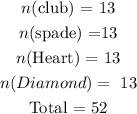
Probability of an event is given as

`Pr=\frac{Number\text{ of }desirable\text{ outcome}}{Number\text{ of total outcome}}`

Probability of choosing a club is evaluated as

`\begin{gathered} Pr(\text{club) = }\frac{Number\text{ of club cards}}{Total\text{ number of playing cards}} \\ Pr(\text{club)}=(13)/(52)=(1)/(4) \\ \Rightarrow Pr(\text{club) = }(1)/(4) \end{gathered}`

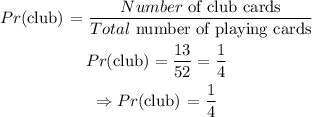
Probability of choosing a spade, without replacement

`\begin{gathered} Pr(\text{spade without replacement})\text{ = }\frac{Number\text{ of spade cards}}{Total\text{ number of playing cards - 1}} \\ =(13)/(51) \\ \Rightarrow Pr(\text{spade without replacement})=(13)/(51) \end{gathered}`

Thus, the probability of both events occuring (choosing a club, and then without replacement a spade) is given as

`\begin{gathered} Pr(\text{club) }*\text{ }Pr(\text{spade without replacement}) \\ =(1)/(4)\text{ }*\text{ }(13)/(51) \\ =(13)/(204) \end{gathered}`

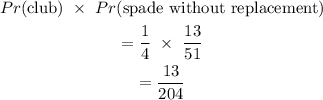
Hence, the probability of choosing a club, and then without replacement a spade is

`(13)/(204)`