Question

Given parallelogram o, p, q, ropqr below, r, s, equals, 51rs=51. if s, p, equals, 2, x, minus, 7sp=2x−7, solve for xx.

Answer 1

`\( x = 29 \)` To solve for
`\( x \)`, you can follow these steps:

Start by using the given information:
`\( 51 = 51 \) and \( 2x - 7 = 2x - 7 \).`

Explaination

Since
`\( 51 = 51 \)`is a true statement, it doesn't provide any specific value for
`\( x \),` so it doesn't affect the solution. Thus, we focus on
`\( 2x - 7 = 2x - 7 \),`which implies that both sides of the equation are equal regardless of the value of
`\( x \).`

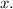
In equations where both sides are identical, any value of
`\( x \)` would satisfy the equation. Hence,
`\( x \)` can take any real number value.

However, if we're looking for a specific value for
`\( x \)` based on the information provided in the problem, we'd need additional constraints or equations to narrow down the possibilities.

Answer 2

The value of x is 16.25

Here's the solution:

1. Identify relevant properties:

Opposite sides of a parallelogram are equal in length (ST = PQ).

The midpoint divides a segment into two segments of equal length (TQ = TP).

2. Apply the properties:

ST = PQ = 51

TQ = TP = 2x - 7

3. Express PQ in terms of x:

PQ = TQ + TP = (2x - 7) + (2x - 7) = 4x - 14

4. Set ST and PQ equal:

51 = 4x - 14

5. Solve for x:

65 = 4x

x = 16.25

Complete the question:

Given parallelogram PQRS below, ST= 51. If TQ = 2x -7, solve for x.