Answer:
Following are the solution to the given question:
Step-by-step explanation:
Please find the complete and correct question in the attachment file.
For Point a:
For the second round,
A is selects kA(2) either 0 or 1, so for each of them, that is
 .
.
B selects
 for each choice with the probability of
for each choice with the probability of
 .
.
If
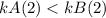 wins the second rear race.
wins the second rear race.
![\to P[A \ wins] = P[kA(2) < kB(2)]](https://img.qammunity.org/2022/formulas/computers-and-technology/college/c0m6iq7flppdxol3z41m9bwln35lkeyf80.png)
![= P[kA(2) = 0] * P[kB(2) > 0] + P[kA(2) = 1] * P[kB(2) > 1]\\\\= (1)/(2) * (3)/(4) + (1)/(2) * (2)/(4) \\\\=(3)/(8) +(2)/(8) \\\\= (3+2)/(8)\\\\= (5)/(8)](https://img.qammunity.org/2022/formulas/computers-and-technology/college/3y5ep4zpy6gd8y156ne0wbb51di4wu2yal.png)
For Point b:
Throughout this example,
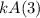 also selects to be either 0 or 1 with such a
also selects to be either 0 or 1 with such a
 probability. So, although B chooses
probability. So, although B chooses
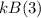 from
from
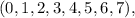 the probabilities each are
the probabilities each are
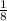 :
:
![\to P[A \ wins] = P[kA(3) < kB(3)]](https://img.qammunity.org/2022/formulas/computers-and-technology/college/q5z3h1rr0kym4gp4glfvwiyygbw0shvd6a.png)
![= P[kA(3) = 0] * P[kB(3) > 0] + P[kA(3) = 1] * P[kB(3) > 1]\\\\= (1)/(2) * (7)/(8) + (1)/(2) * (6)/(8)\\\\= (7)/(16) + (6)/(16)\\\\= (7+6)/(16) \\\\= (13)/(16)\\\\](https://img.qammunity.org/2022/formulas/computers-and-technology/college/vvihfkc9406qb1n56574o6msur3vi6zk5f.png)
For point c:
Assume that B tries again 16 times (typical value), and it destroys. In addition, throughout the exponential background n is obtained at 10 when choosing k between 0 to 2n−1. The probability of A winning all 13 backoff events is:
![P[A \text{wins remaining races}] = 16\pi i =4P[A \ wins \ i |A \ wins \ i -1 ]](https://img.qammunity.org/2022/formulas/computers-and-technology/college/j6i9ngcb74iz8gdkwvje7c2xoretemed6i.png)
Let the k value kA(i) be A for the backoff race I select. Because A retains the breed
![=(kA(i)] \cdot P[kA(i+ 1)< kB(i+ 1)] \geq P[kA(i) + 1<kB(i)] \cdot P[kA(i+ 1)< kB(i+1)]+P[kA(i) + 1 \geq kB(i)] \cdot P[kA(i+ 1)< kB(i+ 1)] \\\\= (P[kA(i) + 1< kB(i)] +P[kA(i) + 1 \geq kB(i)]) * P[kA(i+ 1) < kB(i+ 1)]\\\\=P[kA(i+ 1)< kB(i+ 1)]\\\\](https://img.qammunity.org/2022/formulas/computers-and-technology/college/pkiw8dd6rfjj03p1n4em9al555k7vaku23.png)
For point d:
Two stations A and B are supposed. They assume that B will try 16 times afterward. Even so, for A, 16 races were likely to also be won at a rate of 0.82 For Just higher expectations of three A, B, and C stations. For Station A, possibility to win all backoffs