Question

The lengths of the diagonals of a rhombus are 4.73 and 2.94. What are the measures

of its angles?

Answer 1

Each angle of the rhombus measures approximately 116.91 degrees.

A rhombus is a quadrilateral with all sides equal in length.

The diagonals of a rhombus bisect each other at right angles, meaning that they form four congruent right triangles.

In these right triangles, the hypotenuse is equal to the length of the rhombus' side, and the diagonal is equal to twice the length of one of the right triangle's legs.

Using this information, we can solve for the measures of the angles.

Let's call the length of one side of the rhombus 's'.

The diagonals have lengths of 4.73 and 2.94, which are twice the lengths of the legs of the right triangles.

So we have:

Leg length = 4.73 / 2 = 2.365

Leg length = 2.94 / 2 = 1.47

Now we can use the Pythagorean theorem to find the length of one side of the rhombus:

`s^2 = (2.365)^2 + (1.47)^2`

`s^2 = 5.586225 + 2.1609`

`s^2 = 7.747225\\s = \sqrt{(7.747225)`

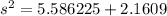
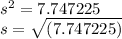
s ≈ 2.78

Since all sides of the rhombus are equal, each angle is equal. We can use the law of cosines to find the measure of one angle:

`cos(A) = (2(2.78)^2 - 4.73^2) / (2(2.78)(2.94))`

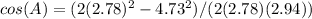
cos(A) = (2(7.7284) - 22.2929) / (16.356)

cos(A) = (15.4568 - 22.2929) / (16.356)

cos(A) = -6.8361 / 16.356

cos(A) ≈ -0.4178

A ≈ arccos(-0.4178)

A ≈ 116.91°

Therefore, the measure of each angle of the rhombus is approximately 116.91°.