Question

Mariah Jacobsen is the marketing manager at ABC Electronics, a major consumer electronics supplier in the northwest. Over the last five years, sales of the company's flagship product - the Wizer Anonymizer (the WA) - have been 45000, 45500, 44500, 46000 and 44000 units. This rate of sales is considered average for the product over the last twenty years or so. Ms. Jacobsen believes that the distribution of the WA's sales is normal with a standard deviation of 1500 units. If she were asked to make a forecast of next year's sales to upper management, what is the likelihood that she would be correct if she predicts sales between 43000 and 46000?

Answer 1

To determine the likelihood of Mariah's sales forecast, we can use the concept of the standard normal distribution and z-scores. The probability that Mariah's forecast will be correct is 68.26%.

Step-by-step explanation:

To determine the likelihood that Mariah Jacobsen will be correct in her forecast of next year's sales, we can use the concept of the standard normal distribution and z-scores.

First, we need to calculate the z-scores for the lower and upper bounds of the predicted sales range:

Zlower = (43000 - 44500) / 1500 = -1

Zupper = (46000 - 44500) / 1500 = 1

Next, we can use a standard normal distribution table or a calculator to find the probabilities associated with these z-scores.

The probability corresponding to a z-score of -1 is approximately 0.1587, and the probability corresponding to a z-score of 1 is approximately 0.8413.

To find the likelihood that the sales will be within the predicted range, we subtract the probability corresponding to the lower bound from the probability corresponding to the upper bound:

0.8413 - 0.1587 = 0.6826 or 68.26%

Answer 2

0.6568 = 65.68% probability that she would be correct.

Step-by-step explanation:

When the distribution is normal, we use the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

45000, 45500, 44500, 46000 and 44000 units. This rate of sales is considered average for the product over the last twenty years or so.

This means that:

`\mu = (45000 + 45500 + 44500 + 46000 + 44000)/(5) = 45000`

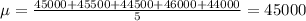
Standard deviation of 1500 units.

This means that
`\sigma = 1500`

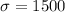
What is the likelihood that she would be correct if she predicts sales between 43000 and 46000?

This is the pvalue of Z when X = 46000 subtracted by the pvalue of Z when X = 43000. So

X = 46000

`Z = (X - \mu)/(\sigma)`

`Z = (46000 - 45000)/(1500)`

`Z = 0.67`

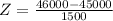
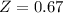
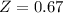`Z = 0.67` has a pvalue of 0.7486

X = 43000

`Z = (X - \mu)/(\sigma)`

`Z = (43000 - 45000)/(1500)`

`Z = -1.33`

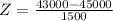
`Z = -1.33` has a pvalue of 0.0918

0.7486 - 0.0918 = 0.6568

0.6568 = 65.68% probability that she would be correct.