Question

In the diagram, BAE is a semicircle, and mZACE = 28° . Based on your explorations, which of the following statements must be true. Select all that apply.

Answer 1

Since the arc BAE is a semicircle, it measures 180°, and the angle that inscribes it, that is, angle ∠BCE, has half the measure, so ∠BCE = 90°.

The angle ∠ACE inscribes the arc AE, so the arc AE has double the measure of the angle ∠ACE, so AE = 56°.

Calculating the measure of the arc AB, we have:

`\begin{gathered} AB+AE=BAE \\ AB+56=180 \\ AB=180-56 \\ AB=124\degree \end{gathered}`

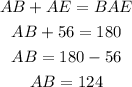
So the first option is correct.

For the second option, these two angles inscribes the same arc (arc AE), so they have the same measure of half the measure of the arc. Therefore, they are congruent, so the second option is correct.

For the third option, there is nothing that proves that these angles are congruent, so the third option is false.

For the fourth option, there is nothing that proves that AC is a diameter, so the fourth option is false.

For the fifth option, the angle ∠BDE inscribes an arc of 180° (semicircle), so it has half the measure of the arc, therefore ∠BDE = 90°. So the fifth option is correct.