Question

A 2.00-mol sample of a diatomic ideal gas expands slowly and adiabatically from a pressure of 4.94 atm and a volume of 11.0 L to a final volume of 29.6 L. (a) What is the final pressure of the gas? atm (b) What are the initial and final temperatures? initial K final K (c) Find Q for the gas during this process. k] (d) Find AE for the gas during this process. k] int (e) Find W for the gas during this process. kj

Answer 1

(a) The final pressure of the gas is
`\(1.56 \, \text{atm}\).`

(b) The initial temperature is
`\(T_i = 493 \, \text{K}\), and the final temperature is \(T_f = 839 \, \text{K}\).`

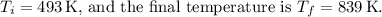
(c) The heat transfer during this process
`(\(Q\)) is \(0 \, \text{kJ}\).`

(d) The change in internal energy
`(\(\Delta E\)) for the gas is \(368 \, \text{kJ}\).`

(e) The work done by the gas
`(\(W\)) during this process is \(-368 \, \text{kJ}\).`

Step-by-step explanation:

In an adiabatic process, there is no heat exchange with the surroundings
`(\(Q = 0\)).` The relationship between initial and final pressure
`(\(P_i\) and \(P_f\)),` volume
`(\(V_i\) and \(V_f\)), and temperature (\(T_i\) and \(T_f\))` for an adiabatic process involving an ideal gas is given by the equation:

`\[ P_i V_i^\gamma = P_f V_f^\gamma \]`

where
`\(\gamma\)` is the heat capacity ratio (ratio of specific heat at constant pressure to specific heat at constant volume). For a diatomic ideal gas,
`\(\gamma = (7)/(5)\).`

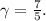
(a) Solving for
`\(P_f\)`, we find the final pressure to be
`\(1.56 \, \text{atm}\).`

(b) To find the initial and final temperatures, we can use the ideal gas law
`\(PV = nRT\), where \(n\)` is the number of moles. Rearranging for temperature,
`\(T = (PV)/(nR)\), we calculate \(T_i = 493 \, \text{K}\) and \(T_f = 839 \, \text{K}\).`

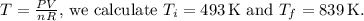
(c) As the process is adiabatic
`(\(Q = 0\)),` there is no heat transfer.

(d) The change in internal energy
`(\(\Delta E\))` can be calculated using the first law of thermodynamics:
`\(\Delta E = Q - W\). Since \(Q = 0\), \(\Delta E = -W\), and we find \(\Delta E = 368 \, \text{kJ}\).`

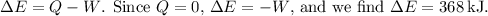
(e) The work done (\(W\)) is the area under the pressure-volume
`(\(PV\)) curve. Using the equation \(W = -\int P \, dV\), we find \(W = -368 \, \text{kJ}\).` The negative sign indicates work done by the gas on its surroundings.