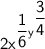Question

Simplify this pretty pls I just can’t figure it out

Answer 1

`\sf 2x^(1)/(6)y^(3)/(4)`

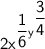
Explanation:

To simplify
`\sf \left( \frac{ 4x^{-(4)/(3) } \cdot 8 y ^(5)/(3)\cdot x }{x^(-1)\cdot 2y ^{-(4)/(3)}} \right)^(1)/(4)`, we can use the definition of exponents and the formula for power and product rule.

The definition of an exponent tells us that
`\sf x^n = x\cdot x\cdot ... \cdot x`,

where n is the number of times we multiply x by itself.

The formula for the product rule tells us that:

`\sf x^n \cdot x^m = x^(n+m)`

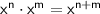
and

Power rule:

`\sf (x^n)^m = x^(nm)`

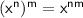
Quotient rule:

`(x^n)/(x^m) = x^(n-m)`

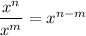
Using these definitions and the formula, we can simplify the expression as follows:

`\sf \left( \frac{ 4x^{-(4)/(3) } \cdot 8 y ^(5)/(3)\cdot x }{x^(-1)\cdot 2y ^{-(4)/(3)}}\right)^(1)/(4) =\left( \frac{ 2^2 \cdot x^{-(4)/(3) } \cdot 2^3 \cdot y ^(5)/(3)\cdot x }{x^(-1)\cdot 2y ^{-(4)/(3)}} \right)^(1)/(4)`

`= \left( \frac{ 2^(2+3) \cdot x^{-(4)/(3)+1 } \cdot y ^(5)/(3) }{x^(-1)\cdot 2y ^{-(4)/(3)}} \right)^(1)/(4)`

`= \left( \frac{ 2^(5) \cdot x^{-(1)/(3) } \cdot y ^(5)/(3) }{x^(-1)\cdot 2y ^{-(4)/(3)}} \right)^(1)/(4)`

`= \left( 2^(5-1) \cdot x^{-(1)/(3) + 1 } \cdot y ^{(5)/(3) +(4)/(3) } \right)^(1)/(4)`

`\left( 2^(4) \cdot x^{(2)/(3) } \cdot y ^{(9)/(3)} \right)^(1)/(4)`

`= \left( 2^(4) \cdot x^{(2)/(3) } \cdot y ^{(9)/(3)} \right)^(1)/(4)`

`= \left( 2^(4) \cdot x^{(2)/(3) } \cdot y ^(3) \right)^(1)/(4)`

`\sf = 2^{4\cdot (1)/(4) } \cdot x^{(2)/(3) \cdot (1)/(4) } \cdot y ^{3\cdot (1)/(4)}`

`= 2 \cdot x^(1)/(6)\cdot y^(3)/(4)`

`= \boxed{2x^(1)/(6)y^(3)/(4)}`

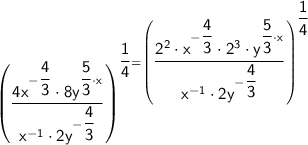
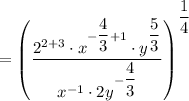
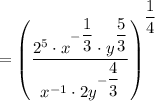
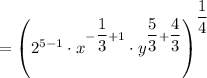
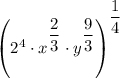
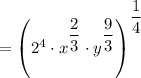
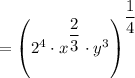
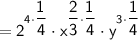
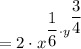
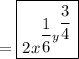
So,

the simplified answer is:

`\sf 2x^(1)/(6)y^(3)/(4)`