Question

mean=100 sd=20 determine the probability that random student scores below 70 on the pax test. above 112 on the pax test, and random student scores between 85 and 115 on the pax test

Answer 1

For this problem, we are given the mean and standard deviation of a certain test. We need to determine a probability of a random sample to be in a few values.

The first value we need to determine is the probability of the random sample being below 70. The first step we need to take is to determine the z-score of this value, which can be calculated with the following expression:

`Z=(x-\mu)/(\sigma)`

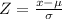
For the value of 70, we have:

`Z=(70-100)/(20)=(-30)/(20)=-1.5`

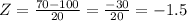
Now we need to find this value on the z-table, which is:

`P(Z<-1.5)=0.0668`

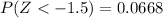
Therefore we can determine that the probability of a value to be below 70 is 6.68%.

Now we need to determine the probability of a value above 112. We need to determine the z-score once again:

`Z=(112-100)/(20)=(12)/(20)=0.6`

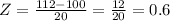
The z-table only tells us values below the z-score, so we need to subtract the result from 1, which is shown below:

`P(Z>0.6)=1-P(Z<0.6)=1-0.7275=0.2725`

The probability of the value being greater than 112 is 27.25%.

Now we need to find the probability of the score to be between 85 and 115. We need to find both Z-scores:

`\begin{gathered} Z(85)=(85-100)/(20)=(-15)/(20)=-0.75\\ \\ Z(115)=(115-100)/(20)=(15)/(20)=0.75 \\ \end{gathered}`

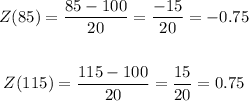
So we need to find the two values on the Z-table and subtract them. We have:

[tex]P(-0.75The probability of the random value being between 85 and 115 is 54.68%.