Let r be the percent annual interest rate of the account. Since $9000 are left for 5 years, for an outcome of $12,500, then:
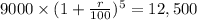
Divide both sides by 9000:
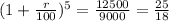
Take the 5th root to both sides:
![\begin{gathered} 1+(r)/(100)=\sqrt[5]{(25)/(18)} \\ \Rightarrow(r)/(100)=\sqrt[5]{(25)/(18)}-1 \\ \Rightarrow r=100(\sqrt[5]{(25)/(18)}-1) \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/rsb0b67ize5i9f7ghndr.png)
Use a calculator to find the decimal expression for r:

Therefore, to the nearest tenth:
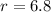
This means that Joshua would need to invest his money on a 6.8% annual interest account.