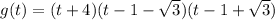Okay, here we have this:
We need to write the following polynomial in factored form as a product of linear factors:
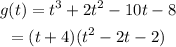
Now, let's solve the following polynomial using the general formula for equations of the second degree:
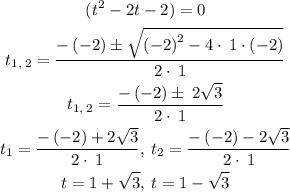
Finally, we obtain the following polynomial: