Question

Can someone help me with this answer

Answer 1

`\sf C.\; x = ((v^2 - v_0^2) )/(2a) + x_0`

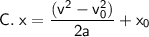
Explanation:

`\sf v^2 = v_0^2 + 2a(x - x_0)`

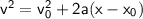
To solve for x in the equation, we can follow these steps:

Subtract
`\sf v _0^2` from both sides:

`\sf v^2 - v_0^2 = v_0^2+2a(x - x_0) - v_0^2`

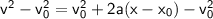
Divide both sides of the equation by 2a:

`\sf ((v^2 - v_0^2) )/(2a) = (2a(x - x_0))/(2a)`

`\sf ((v^2 - v_0^2) )/(2a) = x - x_0`

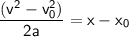
Add
`\sf x_0` to both sides of the equation:

`\sf ((v^2 - v_0^2) )/(2a) + x_0= x - x_0+ x_0`

`\sf ((v^2 - v_0^2) )/(2a) + x_0= x`

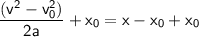
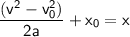
Therefore, the solution for x is:

`\sf C.\; x = ((v^2 - v_0^2) )/(2a) + x_0`

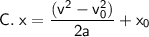
This equation can be used to solve the position of an object moving with constant acceleration, given its initial velocity, final velocity, and acceleration.