Question

What is the common ratio of the geometric sequence below? –2, 4, –8, 16, –32, ...

Answer 1

The common ratio of the geometric sequence is:

`r=-2`

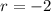
Explanation:

A geometric sequence has a constant ratio 'r' and is defined by

`a_n=a_1\cdot r^(n-1)`

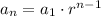
where

• aₙ is the nth term

• a₁ is the first term

• r is the common ratio

Given the sequence

`-2,\:4,-8,\:16,\:-32,\:...`

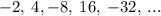
Compute the ratios of all the adjacent terms:
`r=(a_n+1)/(a_n)`

`(4)/(-2)=-2,\:\quad (-8)/(4)=-2,\:\quad (16)/(-8)=-2,\:\quad (-32)/(16)=-2`

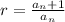
The ratio of all the adjacent terms is the same and equal to

`r=-2`

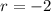
Therefore, the common ratio of the geometric sequence is:

• 
  `r=-2`