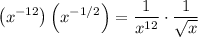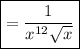1 Answer

Shakthydoss · Answer 1 · 2024-02-22T02:18:17+0000

Answer:

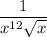
$\displaystyle (1)/(x^(12)√(x))$

Explanation:

We can simplify the expression:

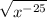
$\displaystyle \sqrt{x^(-25)}$

by rewriting the overarching square root as a power of 1/2:

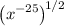
$\displaystyle \left(x^(-25)\right)^(\!1/2)$

This simplifies using the power to a power exponent rule:

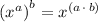
$\left(x^a\right)^b = x^((a\,\cdot\,b))$

↓ applying this rule to the expression

x^(-25/2)

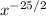
Then, we can separate the whole x's from the fractional x:

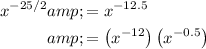
$\displaystyle \begin{aligned}x^(-25/2) &= x^(-12.5) \\ &= \left(x^(-12)\right)\left(x^(-0.5)\right)\end{aligned}$

using the product of powers exponent rule:

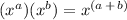
$(x^a)(x^b) = x^((a\,+\,b))$

Finally, the resulting factors can be rewritten without negative or fractional exponents:

$\displaystyle \left(x^(-12)\right)\left(x^(-1/2)\right) = (1)/(x^(12)) \cdot (1)/(√(x))$

$\displaystyle \boxed{=(1)/(x^(12)√(x))}$

Please log in or register to add a comment.