Question

How would you

limit the domain to
make this function
one-to-one and
still have the same
range?
f(x) = x4
-5 -4 -3 -2 -1
x ≥ [?]
8
7
6
5
4
3
2
1
-1
-2
1 2
3
4 5

Answer 1

`x \ge \boxed{0}`

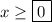
Explanation:

A one-to-one function f(x) is one where, for each value of x there is only one unique value for y and vice-versa

f(x) = x⁴ is not one-to-one function since it is symmetric about the y-axis which means that for a single y value there are two possible values for x. Looking at the graph provided we can see for example that both x = 1 and x = -1 result in the same value for y ie 1

To make the function one-to-one we can restrict the domain to all positive or all negative values (including 0)

So the answer is to limit the domain to
x ≥ 0

(x ≤ 0 also works but is not provided as an answer choice)