Question

For time t≥ 0, the position of a particle is given by s(t) = -t³ + 6t² - 12t+4. What is the velocity when acceleration is zero?

Answer 1

Velocity = 0

Explanation:

The velocity of a particle is the rate of change of its position. It is the derivative of the position function.

The acceleration of a particle is the rate of change of its velocity. It is the derivative of the velocity function.

In this case, the position of the particle is given by the function

s(t) = -t³ + 6t² - 12t+4.

To find the velocity, we need to take the derivative of s(t):

v(t) = ds/dt = -3t² + 12t - 12

To find the acceleration, we need to take the derivative of v(t):

a(t) = dv/dt = -6t + 12

We are asked to find the velocity when acceleration is zero. This means that we need to solve the equation a(t) = 0 for t.

-6t + 12 = 0

-6t = -12

`\sf t = (-12)/(-6)`

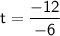
t = 2

Therefore, the velocity when acceleration is zero is v(2). Substituting t = 2 into the expression for v(t), we get:

v(2) = -3(2)² + 12(2) - 12

v(2) = -12 + 24 - 12

v(2) = -24 + 24

v(2) = 0

Therefore, the velocity of the particle when acceleration is zero is 0.