Given:
Rita earns scores of 83, 87, 85, 88, and 90 on her five-chapter tests for a certain class.
And a grade of 82 on the class project.
First, we will find the average of the scores of the five tests

The overall average for the course is computed as follows:
30% of the course grade ⇒ Rita get 86.6
30% of project grade ⇒ Rita get 82
40% of the final exam ⇒ let Rita get x
We will find the value of x provided that Rita will earn a "B" score
a "B" is an overall score greater than or equal to 80, but less than 90
So, we will find (x) as follows:
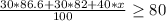
Solve the inequality to find (x):
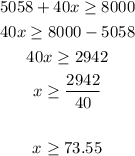
And the upper limit will be as follows:
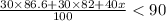
Solve to find (x):

So, the answer will be:
To obtain a "B", Rita needs to score between 73.55 and 98.55