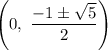Question

X^2+x-1

how to find x-intercepts

Answer 1

`\left(0,\ (-1\pm\sqrt5)/(2)\right)`

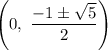
Explanation:

The x-intercept of a function is the point when the function crosses the x-axis.

The x-axis is defined by the equation:

• y = 0

So, we can solve for the x-coordinates of the function's x-intercepts by substituting 0 for y in the function definition:

y = x² + x - 1

0 = x² + x - 1

From here, we can solve for x by completing the square:

↓ adding 1 to both sides

1 = x² + x

↓ adding (1/2)² to both sides ... To get that added number, we take the x term's coefficient (in this case, 1), divide it by 2, then square it.

5/4 = x² + x + 1/4

↓ factoring the right side as a perfect square

5/4 = (x + 1/2)²

↓ taking the square root of both sides

±
`\sqrt5`/2 = x + 1/2

↓ subtracting 1/2 from both sides

x = -1/2 ±
`\sqrt5`/2

↓ combining fractions with the same denominator

`x = (-1\pm\sqrt5)/(2)`

So, the x-intercepts of the function

• y = x² + x - 1

are:

`\left(0,\ (-1\pm\sqrt5)/(2)\right)`