Question

Assume the acceleration of the object is a(t) = −32 feet per second per second. (Neglect air resistance.) With what initial velocity must an object be thrown upward (from ground level) to reach the top of a national monument (590 feet)? (Round your answer to three decimal places.) ______ft/sec?

Answer 1

The initial velocity required to reach the top of a national monument can be found using the equation
`Vf^2 = Vi^2 + 2ad,` where Vf is the final velocity, Vi is the initial velocity, a is the acceleration, and d is the displacement. Substituting the given values and solving for Vi, we find that it must be approximately 94.221 ft/sec.

Step-by-step explanation:

To find the initial velocity required for an object to reach the top of a national monument, we can use the following equation:

`Vf^2 = Vi^2 + 2ad`

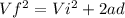
• Vf is the final velocity, which is 0 at the top of the monument
• Vi is the initial velocity, which we are trying to find
• a is the acceleration, which is -32 feet per second squared in this case
• d is the displacement, which is 590 feet

Substituting the values into the equation and rearranging it, we get:

`Vi^2 = 2ad`

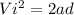
Plugging in the values, we have:

`Vi^2 = 2(-32)(590)`

Solving for Vi, we find the initial velocity must be approximately 94.221 ft/sec.

Learn more about initial velocity