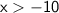Answer:
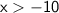
Explanation:
To solve the inequality
 ,we can follow these steps:
,we can follow these steps:
First, let's get rid of the fractions by multiplying both sides of the inequality by 5 to clear the denominator:
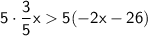
This simplifies to:
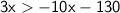
Now, let's gather like terms on each side of the inequality.
Add 10x to both sides to move all the x-terms to the left side:
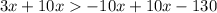
This simplifies to:
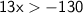
Finally, divide both sides by 13 to isolate x:
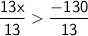
This simplifies to:
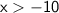
So, the solution to the inequality is: