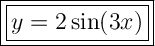Answer:
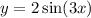
Explanation:
The provided graph shows a sinusoidal function. Since the curve passes through the origin (0, 0), we will use the general form of the sine function to identify the equation of the graph.
The general form of the sine function is:

where:
- A is the amplitude.
- 2π/B is the period.
- C is the phase shift.
- D is the vertical shift.
The amplitude of a sinusoidal function is one-half of the positive difference between the maximum and minimum values of a function.
The maximum value is 2 and the minimum value is -2. Therefore:
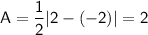
The period is the horizontal length of one cycle of the curve. From observation of the given graph, the period is 2π/3. Therefore:
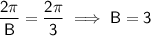
The phase shift is the horizontal shift. There is no horizontal shift, so:
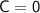
The midline is the horizontal line located at a y-value that is midway between the maximum (peak) and minimum (trough) y-values of the function. Since the maximum y-value is 2 and the minimum y-value is -2, the midline of the graphed function is y = 0.
The midline of the parent sine function y = sin(x) is the x-axis (y = 0), so the graphed function has undergone no vertical shift:
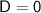
Substitute the found values of A, B, C and D into the formula:
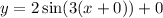
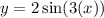
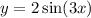
Therefore, the equation of the graphed function is: