Answer:
a)
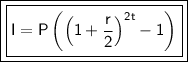
b) Rs 19475
c) Rs 21645.12
d) Rs 2170.12
e) 11.14%
Explanation:
Given:
- Principal (P) = Rs 2,00,000
For 1st year
- Tax reduced = Rs 5%
- Rate(r) = 10% per annum semi annually
For 2nd year
- Rate(r) = 10% per annum semi annually with out Tax
Solution:
a) Formula for semi-annual compound interest:
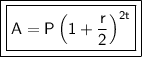
where:
- A is the final amount
- P is the principal amount
- r is the annual interest rate in decimal form (10% = 0.10)
- t is the time in years

b) Interest of the first year after deducting tax by subtracting tax amounts from interest.
We can get interest by using formula:
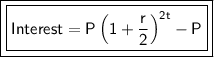
Substitute the given value and simplify it:

Now, we have
Interest deducting the tax = Interest - tax% of Interest
= Rs 20500 - 5% of Rs 20500
= Rs 20500 - 0.05 × Rs 20500
= Rs 20500 - Rs 1025
= Rs 19475
Therefore, Interest deducting the tax is Rs 19475.

c) Interest of the second year after deducting tax:
Since the bank has changed the policy to accomplish the interest terminally at the same rate of interest, we will need to use the following formula to calculate the interest of the second year:

New principal will be Interest + previous principal
= Rs 19475 + Rs 200000
= Rs 219475 ( 1+ 0.10) - 219475
Substitute the given value and simplify it:

Now, we have
Interest deducting the tax = Interest - tax% of Interest
= Rs 22784.33 - 5% of Rs 22784.33
= Rs 22784.33 - 0.05 × Rs 22784.334169921875
= Rs 22784.33 - Rs 1139.21
= Rs 21645.12
Therefore, Interest deducting the tax is Rs 21645.12

d) Difference between the interest of the first year and the second year after deducting the tax:
Difference = Interest of the second year - Interest of the first year
Difference = 21645.12 - 19475
Difference = Rs 2170.12
So, the difference in interest is Rs 2170.12

e) Percentage difference between the interest of the first year and the second year after deducting the tax:

So, the percentage difference is 11.14%