Question

PLS HELP DON'T KNOW REALLY NEED IT.

Answer 1

B. Rhombus

Explanation:

Use the distance formula to calculate the distances between two points.

Distance = √(x2-x1)^2 + (y2-y1)^2

Answer 2

B. Rhombus

Explanation:

To determine if the provided figure is a square, rhombus, trapezoid or rectangle, we need to analyse its side lengths, side parallelism, and interior angles.

As the x-coordinates of points B, A and D are 0, a and 2a respectively, the horizontal distance from A to B and from A to D is the same ("a" units). As the y-coordinates of points B and D are the same, this means that AB = AD.

As the x-coordinates of points B, C and D are 0, a and 2a respectively, the horizontal distance from B to C and from C to D is the same ("a" units). As the y-coordinates of points B and D are the same, this means that BC = CD.

As the y-coordinates of points A, B and C are 0, b and 2b respectively, the vertical distance from A to B and from B to C is the same ("b" units). As the x-coordinates of points A and C are the same, this means that AB = BC.

If AB = AD, BC = CD and AB = BC, then AB = BC = CD = AD. Therefore, all four sides of the figure are congruent.

From this information, we can also derive that AB is parallel to CD, and AD is parallel to BC. Additionally, we can say that the diagonals (AC and BD) of the figure are perpendicular.

Assuming a ≠ b, the interior angles cannot be right angles.

To summarise:

• All four sides of the figure are congruent.
• The opposite sides of the figure are parallel.
• The diagonals are perpendicular
• The interior angles are not right angles.

Therefore, the figure must be a:

`\Large\boxed{\boxed{\sf Rhombus}}`

The figure is not a square because although a square has four sides of equal length, its interior angles are all right angles. (Note that if a = b, then it would be a square).

The figure is not a rectangle as its four sides are the same length. A rectangle has two pairs of congruent, parallel sides, but each pair has different lengths.

The figure is not a trapezoid because it has two pairs of parallel sides. A trapezoid only has one pair of parallel sides, and the other two sides are non-parallel.

`\hrulefill`

We can prove that the side lengths are equal in length by using the distance formula.

`\boxed{\begin{array}{l}\underline{\sf Distance \;Formula}\\\\d=√((x_1-x_2)^2+(y_1-y_2)^2)\\\\\textsf{where:}\\ \phantom{ww}\bullet\;\;d\;\textsf{is the distance between two points.} \\\phantom{ww}\bullet\;\;\textsf{$(x_1,y_1)$ and $(x_2,y_2)$ are the two points.}\\\\\end{array}}`

Therefore:

`\begin{aligned}AB&=√((x_A-x_B)^2+(y_A-y_B)^2)\\&=√((a-0)^2+(0-b)^2)\\&=√((a)^2+(-b)^2)\\&=√(a^2+b^2)\end{aligned}`

`\begin{aligned}BC&=√((x_B-x_C)^2+(y_B-y_C)^2)\\&=√((0-a)^2+(b-2b)^2)\\&=√((-a)^2+(-b)^2)\\&=√(a^2+b^2)\end{aligned}`

`\begin{aligned}CD&=√((x_C-x_D)^2+(y_C-y_D)^2)\\&=√((a-2a)^2+(2b-b)^2)\\&=√((-a)^2+(b)^2)\\&=√(a^2+b^2)\end{aligned}`

`\begin{aligned}AD&=√((x_A-x_D)^2+(y_A-y_D)^2)\\&=√((a-2a)^2+(0-b)^2)\\&=√((-a)^2+(-b)^2)\\&=√(a^2+b^2)\end{aligned}`

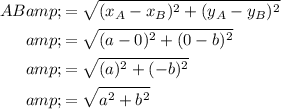
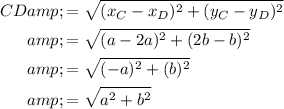
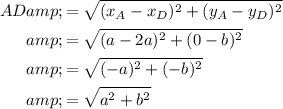
Thus proving that AB = BC = CD = AD.