Answer:
c) perpendicular lines
Explanation:
Given equation:
- 4x - 2y = -5 Green line
 Red line
Red line
We can rewrite the first equation in slope-intercept form:

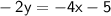

This gives us the slope and y-intercept of the first line, which are 2 and 5/2, respectively.
The second equation is already in slope-intercept form, with a slope of -1/2 and a y-intercept of -1/10.
Since the slopes are not equal, the lines are not the same. The slope of the first equation is 2, and the negative reciprocal of 2 is -1/2, which is the slope of the second equation.
Therefore, the two lines are perpendicular.
so, the answer is c) perpendicular lines