Question

What is the distance between point A(-8,-4) and point B(2,-4)

Answer 1

10

Explanation:

Use distance formula:

d =
`\sqrt{(x_(2) - x_(1))^2 + (y_(2) - y_(1))^2}`

Where (x1, y1) represent the first set of coordinates and (x2, y2) the second pair.

We are given:

A(-8, -4)

and

B(2, -4)

Let's call the coordinates of point A our first set and the coordinates of point B our second.

Plug them into the formula:

d =
`\sqrt{(x_(2) - x_(1))^2 + (y_(2) - y_(1))^2}`

Becomes:

d =
`√((2 - (-8))^2 + (-4 - (-4))^2)`

Simplify inside the parenthesis first according to PEMDAS:

d =
`√((10)^2 + (0)^2)`

Solve exponents now:

d =
`√(100 + 0)`

d =
`√(100)`

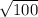
Two numbers equal to each other that multiply to 100 is 10, so:

d = 10

The distance between points A(-8, -4) and B(2, -4) is 10.