Question

Express x2+6x in the form (x+a)2+ b where a and b are numbers

Answer 1

`\displaystyle{y = {(x + 3)}^(2) - 9}`

Explanation:

Given the function:

`\displaystyle{y = {x }^(2) + 6x}`

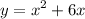
We want to express it in the vertex form:

`\displaystyle{y = {(x - a)}^(2) + b}`

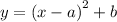
First, find the constant term "n" that can convert x² + 6x + n to perfect square. We can find it by applying the formula:

`\displaystyle{n = { \left( \frac{ \text{middle term}}{2} \right)}^(2) }`

Thus:

`\displaystyle{n = { \left( (6)/(2) \right)}^(2) } \\ \\ \displaystyle{n = {3}^(2) } \\ \\ \displaystyle{n = 9}`

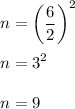
Therefore, the constant term is 9. Hence, we rewrite the equation as:

`\displaystyle{y = {x}^(2) + 6x + 9 - 9}`

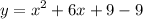
We have to subtract 9 too or else the equation will not equal to the original. Keep in mind that:

`\displaystyle{ {x}^(2) + 6x = {x}^(2) + 6x + 9 - 9} \\ \displaystyle{ \text{but} \: {x}^(2) + 6x \\eq {x}^(2) + 6x + 9 }`

Then we complete the square while remaining -9 outside:

`\displaystyle{y = {(x + 3)}^(2) - 9}`