Question

The diagram shows three circles, each of radius 6 cm.

The centres of the circles are A, B and C such that
ABC is an equilateral triangle.
Work out the total area of the three shaded regions.
Give your answer in terms of pie

Answer 1

Explanation:

First find the area of the curved triangle ABC.

This consists of an equilateral triangle + 3 circle segments on each of its sides.

Area of triangle = 1/2 *6^2 * sin 60

= 18 sin 60

= 18 √3/2

= 9√3.

Area of 1 segment = area of a sector - area of the triangle

= 1/6 * π * 6^2 - 9√3

= 6π - 9√3

So the total area of ABC = 9√3 + 3( 6π - 9√3)

= 18π - 18√3

Area of shaded regions = area of the circle Centre C - area of ABC

= π(6)^2 - (18π - 18√3)

= 18π + 18√3

= 18(π + √3)

Answer 2

The total area of the three shaded regions is 72π + 27√3
`cm^2`.

To find the total area of the three shaded regions, we can break down the problem into smaller components.

Each shaded region is formed by two sectors of the circles and an equilateral triangle.

1. Sector area:

The angle of each sector can be found by dividing the central angle of the equilateral triangle (which is 360 degrees) by 3. Thus, each sector has an angle of 120 degrees.

The formula for the area of a sector is (angle/360) * π *
`radius^2`.

For each circle with a radius of 6 cm, the area of one sector would be (120/360) * π *
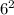`6^2` = 12π
`cm^2`.

2. Equilateral triangle area:

The formula for the area of an equilateral triangle is (
`side length^2` * √3) / 4.

Since each side of the equilateral triangle is the same length as the radius of the circles (6 cm), the area of the equilateral triangle is (
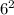`6^2` * √3) / 4 = 9√3
`cm^2`.

3. Total area of one shaded region:

Adding the area of the two sectors and the area of the equilateral triangle, the total area of one shaded region is 24π + 9√3
`cm^2`.

4. Total area of the three shaded regions:

Since there are three shaded regions in total, the total area of the three shaded regions is 3 * (24π + 9√3) = 72π + 27√3
`cm^2`.

Therefore, the total area of the three shaded regions is 72π + 27√3
`cm^2`.