Question

Question 6 - Pythagoras and Trigonometry

The diagram shows a quadrilateral ABCD.
A
15cm
11cm
B
881001
37⁰
C

Answer 1

CD = 16.9 cm

Explanation:

Length of BD

To calculate the length of CD, we first need to determine the length of BD. Since triangle ABD is a right triangle, we can use Pythagoras Theorem to calculate the length of BD.

Given the legs of ΔABD are BD and AD, and the hypotenuse is AB, then:

`BD^2+AD^2=AB^2`

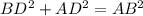
Substitute AD = 11 cm and AB = 15 cm, and solve for BD:

`BD^2+11^2=15^2`

`BD^2+121=225`

`BD^2=104`

`BD=√(104)`

`BD=√(4\cdot 26)`

`BD=√(4)√(26)`

`BD=2√(26)`

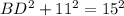
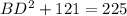
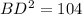
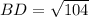
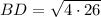
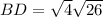
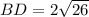
Length of CD

Side CD is the hypotenuse of triangle BCD. Since we know the length of side BD and the measure of the angle opposite BD, we can use the sine trigonometric ratio to find the length of CD.

`\boxed{\begin{array}{l}\underline{\textsf{Sine trigonometric ratio}}\\\\\sf \sin(\theta)=(O)/(H)\\\\\textsf{where:}\\\phantom{ww}\bullet\;\textsf{$\theta$ is the angle.}\\\phantom{ww}\bullet\;\textsf{O is the side opposite the angle.}\\\phantom{ww}\bullet\;\textsf{H is the hypotenuse (the side opposite the right angle).}\end{array}}`

In this case:

• θ = 37°
• O = BD = 2√(26) cm
• H = CD

Substitute these values into the sine ratio:

`\sin(37^(\circ))=(2√(26))/(CD)`

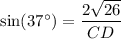
Solve for CD:

`CD=(2√(26))/(\sin(37^(\circ)))`

`CD=16.9454710...`

`CD=16.9\; \sf cm\;(3\;s.f.)`

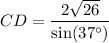
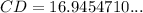
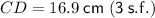
Therefore, the length of CD is 16.9 cm (rounded to three significant figures).