Question

If twice the son's age in years is added to the father's age, the sum is 70. Bul twice

the father's age is added to the son's age, the sum is 95.
(i) Express the above statements in the form of linear equations.
(ii) Find the present ages of the father and his son.

Answer 1

Father's age = 40 years

Son's age = 15 years

Explanation:

Framing linear equations and solving:

Let the father's age be 'x' and son's age be 'y'.

Twice the son's age is two times of y and it is denoted by 2y.

Sum of x and 2y is 70.

x + 2y = 70 ----------------------(I)

Twice the father's age is two times of 'x' and it is denoted by 2x

Sum of 2x any y is 95.

2x + y = 95 ------------------(II)

Linear equations:

x + 2y = 70 ------------(I)

2x + y = 95 ------------(II)

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~`

(II) We can use substitution method to solve the linear equations.

x + 2y = 70

x = 70 - 2y --------------(III)

Substitute x = 70 - 2y in equation (I),

2*(70-2y) + y = 95

2*70 - 2*2y + y = 95

140 - 4y + y = 95

Combine the like terms, -4y and y,

140 - 3y = 95

Subtract 140 from both sides,

-3y = 95 - 140

-3y = - 45

Divide both sides by (-3),

y = (-45) ÷ (-3)

`\boxed{\bf y = 15 }`

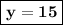
Substitute y = 15 in equation (III),

x = 70 - 2*15

= 70 - 30

`\sf \boxed{\bf x = 40}`

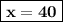
Answer: Father's age = 40 years

Son's age = 15 years