Question

A cold air-standard Otto cycle has a compression ratio of 6 and the temperature and pressure at the beginning of the compression process are 520°R and 14.2 lbf/in.2, respectively. The heat addition per unit mass of air is 400 Btu/Ib. Assume constant specific heats evaluted at 520°R. Determine: (a) the maximum temperature, in °R.

Answer 1

The maximum temperature in a cold air-standard Otto cycle can be determined using the given information and the equation
`TV^(y-1) =`constant. The maximum temperature is found to be 1711.55°R.

Step-by-step explanation:

The maximum temperature in a cold air-standard Otto cycle can be determined using the given information. The compression ratio is 6, and the temperature at the beginning of the compression process is 520°R. In an Otto cycle, the maximum temperature occurs at the end of the compression process when the gas is at its smallest volume. The relationship between temperature and volume for an adiabatic process is described by the equation
`TV^(y-1) =`constant, where T is the temperature, V is the volume, and y is the specific heat ratio. Since the specific heat ratio for air is 7/5, we can use this equation to find the maximum temperature.

Using the given values, we can set up the equation as follows:

Since the compression ratio is 6, V1/V2 = 6, so we can substitute 6 for V1/V2:

(520°R)
`(6)^(7/5-1) = (Tmax)(1)^(7/5-1)`

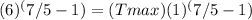
Simplifying the equation, we get:

520°R *
`36^(2/5) = Tmax`

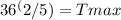
Calculating the right side of the equation, we find:

520°R * 3.3019 = Tmax

Tmax = 1711.55°R

Therefore, the maximum temperature in the cold air-standard Otto cycle is 1711.55°R.

Answer 2

The maximum temperature in the air-standard Otto cycle is approximately 1729°R.

PV^(γ) = constant

where γ is the specific heat ratio (Cp/Cv).

Using the ideal gas law (PV = nRT), we can eliminate volume terms and express pressure as a function of temperature:

P_2 = P_1 * (T_2/T_1)^(γ)

Applying to Process 1-2:

P_1 = 14.2 lbf/in² and r = 6.

T_2 = T_1 * r(γ-1) = 520°R * 6(γ-1)

for Process 2-3:

ΔT_23 = Q_in / Cv

T_3 = T_2 + ΔT_23

= T_2 + 400Btu/lb / Cv

for Process 3-4:

T_4 = T_3 *

The maximum temperature occurs at state 3. and T_max = T_3. For air at typical temperatures, γ = 1.4 and Cv = 0.17 Btu/lb°R.

T_2 = T_1 * r(γ-1) = 520°R * 6(γ-1)

T-2 = 1729°R.