Question

Consider a symmetrical square wave of 5-V peak-to-peak, 0 average, and 2-us period applied to a Miller integrator. Find the value of the time constant CR such that the triangular waveform at the output has a 5-V peak-to-peak amplitude.

Answer 1

The value of the time constant CR in the given Miller integrator circuit is 0.736 us.

Step-by-step explanation:

The time constant of an RC circuit is given by the formula t = RC, where R is the resistance and C is the capacitance. In this case, we need to find the value of the time constant CR such that the triangular waveform at the output has a 5-V peak-to-peak amplitude. Given that the square wave has a 5-V peak-to-peak amplitude, we can start by finding the time it takes for the voltage to decline to half of its peak value. This is known as the time constant. For a symmetrical square wave with a period of 2 us, the time constant can be found by multiplying the time period by 0.368, which gives us 0.736 us. So, the value of the time constant CR is 0.736 us.

Answer 2

The value of the time constant CR such that the triangular waveform at the output has a 5-V peak-to-peak amplitude is 0.5μs

How to determine the value of the time constant CR such that the triangular waveform at the output has a 5-V peak-to-peak amplitude?

In order to do this, we use the formula;

`V = (1)/(RC) \int\limits^t_0 {vin} \, dt`

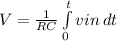
So;

`5= (1)/(RC) \int\limits_0^\(1 *10^\(-6\) {2.5} \,dt`

`5=(1)/(RC) * 2.5 * 10^\(-6\)`

`RC=0.5 * 10^\(-6\)`

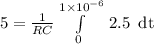
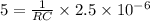
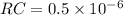
Time Constant = Rc = 0.5μs

Therefore, the value of the time constant CR such that the triangular waveform at the output has a 5-V peak-to-peak amplitude is 0.5μs

See the attached image for missing part of question