Question

Question is attached

Answer 1

Answer:
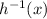`h^(-1)(x)` = (-4x - 1) / (2-x), range:
`(-\infty, \infty)`

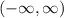
Explanation:

1. To find the inverse of h(x), swap the x's and y's: x = (2y + 1) / (y-4)
2. Use algebra to make y be by itself on one side of the equals sign:

• x(y-4) = 2y + 1
• xy - 4x - 1 = 2y
• -4x - 1 = 2y - xy
• -4x - 1 = y(2-x)
• y = (-4x - 1) / (2 - x), which is your inverse of h(x) that we call h^(-1)(x)

This is a hyperbolic function with an vertical asymptote at x = 2, so its range is
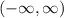`(-\infty, \infty)`. That is, the range of our inverse function contains all y ∈ R