Question

Which graph represents the solution to the system of inequalities?

Answer 1

Graph B (see attached).

Explanation:

Given system of inequalities:

`\begin{cases}y < -2x+1\\y\leq 3x-2\end{cases}`

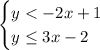
When graphing inequalities:

• Use a dashed line for < or >.
• Use a solid line for ≤ or ≥.
• Shade below the line for < or ≤.
• Shade above the line for > or ≥.

Inequality y < -2x + 1

• The "<" sign indicates a dashed line with shading below the line.
• The slope of the line is negative, so the dashed line slopes downward from left to right.
• The y-intercept is 1, so the dashed line will intercept the y-axis at y = 1.

Inequality y ≤ 3x - 2

• The "≤" sign indicates a solid line with shading below the line.
• The slope of the line is positive, so the sold line slopes upward from left to right.
• The y-intercept is -2, so the solid line will intercept the y-axis at y = -2.

All of the given answer options show the correctly graphed dashed and solid boundary lines. So, we are looking for the graph that has shading below both the dashed line and the solid line. Therefore, the graph that satisfies this is represented by option B.