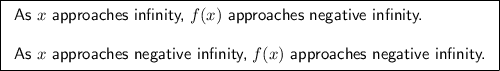Question

PLS HELP
What is the end behavior of the graph?

Answer 1

`\textsf{A)}\quad \boxed{\begin{array}{l}\textsf{As $x$ approaches infinity, $f(x)$ approaches negative infinity.}\\\\\textsf{As $x$ approaches negative infinity, $f(x)$ approaches negative infinity.}\end{array}}`

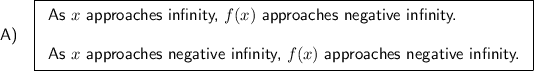
Explanation:

The end behavior of a function refers to the behavior of the function's values as the input (x-values) approaches positive or negative infinity.

The graphed function is a downward-opening parabola with a vertex at (0, 0) and an axis of symmetry at x = 0.

From observation of the graphed function:

• As x approaches positive infinity (+∞), the function approaches negative infinity (-∞). In other words, as x becomes very large on the positive side, the function decreases without bound.
  
  
• As x approaches negative infinity (-∞), the function also approaches negative infinity (-∞). Similarly, on the negative side, as x becomes very large in the negative direction, the function decreases without bound.

Therefore, the end behavior of the function is:

`\boxed{\begin{array}{l}\textsf{As $x$ approaches infinity, $f(x)$ approaches negative infinity.}\\\\\textsf{As $x$ approaches negative infinity, $f(x)$ approaches negative infinity.}\end{array}}`