Answer:
sin(2u) = - 8/17
cos(2u) = 15/17
tan(2u) = -8/15
Explanation:
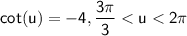
To find the exact values of sin(2u), cos(2u), and tan(2u) using the double-angle formulas, we will need to know the value of sin(u) and cos(u).
We can use the Pythagorean identity to find sin(u) and cos(u):
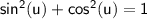
Since cot(u) = -4, we know that cos(u) / sin(u) = -4. We also know that cos(u) > 0 because u is in the third quadrant. Therefore, we can say that:

Substituting this into the Pythagorean identity, we get:
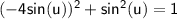
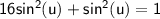

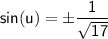
Since u is in the third quadrant, we know that sin(u) is negative.
Therefore,
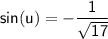
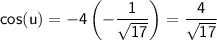
Now that we know sin(u) and cos(u), we can use the double-angle formulas to find sin(2u), cos(2u), and tan(2u):
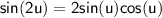
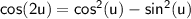
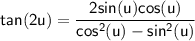
Substituting in
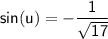 and
and
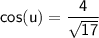 , we get:
, we get:
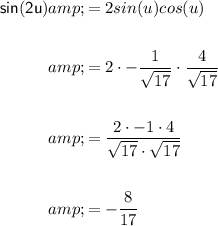
Now

And Finally:
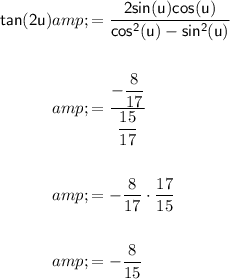
Therefore, the exact values of sin(2u), cos(2u), and tan(2u) are:
sin(2u) = - 8/17
cos(2u) = 15/17
tan(2u) = -8/15