Question

Find the exact value

asked Feb 13, 2024 109k views

1 Answer

Ask a Question

Gisellet · Answer 1 · 2024-02-18T02:00:45+0000

Answer:

a) sin(θ) = 5/13

b) cos(θ) = 12/13

c) tan(θ) = 5/12

d) cos(2θ) =119/169

e) tan(2θ) = 120/119

f) cot(2θ) = 119/120

g) sec(2θ) = 169/119

h) csc(2θ) = 169/120

Explanation:

Given:

With respect to θ.

Opposite = 5
Adjacent = 12

To find:

a) sin(θ)
b) cos(θ)
c) tan(θ)
d) cos(2θ)
e) tan(2θ)
f) cot(2θ)
g) sec(2θ)
h) csc(2θ)

Solution:

First let's find hypotenuse by using Pythagorean theorem:

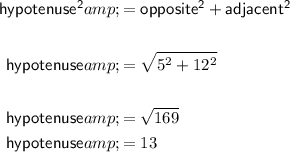
$\begin{aligned} \sf hypotenuse^2 & =\sf opposite ^2 + adjacent ^2 \\\\ \sf hypotenuse & = √( 5^2 + 12^2 ) \\\\ \sf hypotenuse & = √(169)\\\ \sf hypotenuse & = 13 \end{aligned}$

Now,

Let's find all

a) sin(θ)

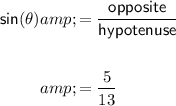
$\begin{aligned} \sf sin(\theta) & =\sf (opposite )/( hypotenuse )\\\\ & = (5 )/(13) \end{aligned}$

b) cos(θ)

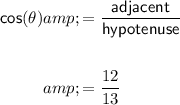
$\begin{aligned} \sf cos(\theta) & =\sf ( adjacent )/( hypotenuse ) \\\\ & =( 12 )/( 13) \end{aligned}$

c) tan(θ)

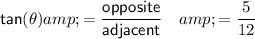
$\begin{aligned} \sf tan(\theta) & =\sf (opposite )/( adjacent ) & = (5)/(12)\end{aligned}$

d) cos(2θ)

To find cos(2θ), we can use the following formula:

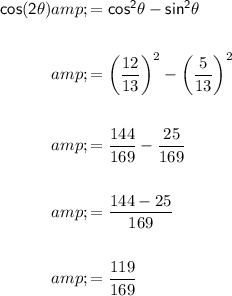
$\begin{aligned} \sf cos(2\theta) & = \sf cos^2 \theta - sin^2 \theta \\\\ & = \left((12)/(13)\right)^2 - \left((5)/(13)\right)^2 \\\\ & = (144)/(169) - (25)/(169) \\\\ & = (144 - 25 )/(169) \\\\ & = (119)/(169) \end{aligned}$

e) tan(2θ)

To find tan(2θ), we can use the following formula:

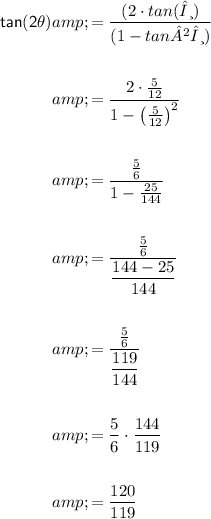
$\begin{aligned} \sf tan(2\theta )& =( (2 \cdot tan(θ))/( (1 - tan²θ)) \\\\ & = ( 2 \cdot ( 5 )/( 12))/(1 -\left((5)/(12)\right)^2 ) \\\\ & = ( (5)/(6) )/( 1 - (25)/(144)) \\\\ & = ((5)/(6))/(( 144 - 25)/(144)) \\\\ & = ((5)/(6))/(( 119)/(144)) \\\\ & = (5)/(6)\cdot ( 144)/(119) \\\\ & = (120)/(119)\end{aligned}$

f) cot(2θ)

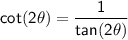
$\sf cot(2\theta ) =( 1 )/( tan(2\theta))$

Therefore,

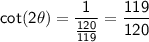
$\sf cot(2\theta ) =( 1 )/( (120)/(119)) = (119)/(120)$

g) sec(2θ)

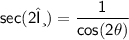
$\sf sec(2θ) =( 1 )/(cos(2\theta) )$

Therefore,

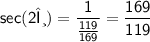
$\sf sec(2θ) =( 1 )/((119)/(169) ) =(169)/(119)$

f) csc(2θ)

$\sf csc(2\theta) =( 1 )/( sin(2\theta))$

To find sin(2θ), we can use the following formula:

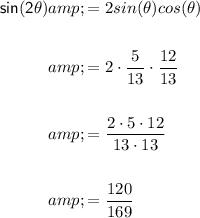
$\begin{aligned} \sf sin(2\theta) & = 2 sin(\theta) cos(\theta) \\\\ & = 2 \cdot (5 )/( 13)\cdot (12 )/(13) \\\\ & = ( 2 \cdot 5 \cdot 12 )/(13\cdot 13 ) \\\\ & = (120)/( 169)\end{aligned}$

$\sf csc(2\theta) =( 1 )/( (120)/(169)) = (169)/(120)$

So, the answer is: