Question

Calculate the future value. (Round your answer to two decimal places.)

P = $24,000, r = 4% compounded monthly, t = 4 years

Answer 1

Future value ≈ $28,156.77

Explanation:

The formula for the future value of an investment with compound interest is given by:

`FV=P(1+(r)/(n))^(^n^t^)`, where:

• FV is the future value,
• P is the principal (aka the deposit,
• r is the interest rate (as a decimal),
• n is the number of compounding periods,
• and t is the time in years.

Identifying the variables:

We're solving for A and already know that:

• P = $24000,
• r = 0.04,
• n = 12 (because there are 12 months in a year, the money is compounded once every month),
• and t = 4

Now, we can solve for FV by substituting these values for P, r, n, and t in the compound interest formula:

`FV=24000(1+(0.04)/(12))^(^1^2^*^4^)\\ \\FV=24000(1+(1)/(300))^(^4^8^)\\ \\FV=24000(301/300)^(^4^8^)\\\\FV=28156.76808\\\\FV=28156.77`

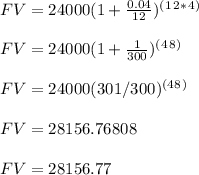
Therefore, future value is about about $28,156.77.