Question

Determine the amplitude, period, and phase shift for y=1/3tan (0 +30) and use them to plot the graph of the function.

Answer 1

Given: The function below

`y=(1)/(3)tan(\theta+30^0)`

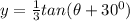
To Determine: The amplitude, the period, and the phase shift

Solution

The graph of the function is as shown below

The general equation of a tangent function is

`f(x)=Atan(Bx+C)+D`

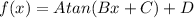
Where

`\begin{gathered} A=Amplitude \\ Period=(\pi)/(B) \\ Phase-shift=-(C)/(B) \\ Vertical-shift=D \end{gathered}`

Let us compare the general form to the given

`\begin{gathered} y=(1)/(3)tan(\theta+30^0) \\ f(x)=Atan(B\theta+C)+D \\ A=(1)/(3) \\ B=1 \\ C=30^0 \\ D=0 \end{gathered}`

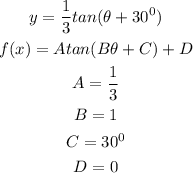
Therefore

`\begin{gathered} Amplitude=(1)/(3) \\ Period=(\pi)/(B)=(180^0)/(1)=180^0 \\ Phase-shift=-(C)/(B)=-(30^0)/(1)=-30^0 \end{gathered}`

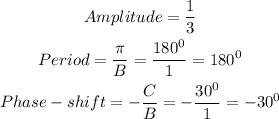
Hence, the correct option is as shown below