Question

\[\begin{aligned} f(x)&=x^2 \\\\ g(x)&=(x - 6)^2 \end{aligned}\] We can think of \[g\] as a translated (shifted) version of \[f\]. Complete the description of the transformation. Use nonnegative numbers. To get the function \[g\], shift \[f\] by units. Stuck?

Answer 1

To get the function g, shift by 6 units

Explanation:

To see this, we can perform the following shift:

`\begin{aligned} f(x) &= x^2 \\\\ f(x + h) &= (x + h)^2 \\\\ &= (x^2 + 2hx + h^2) \\\\ &= x^2 + 2hx + h^2 \end{aligned}`

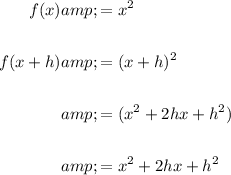
Setting this expression equal to $g(x)$, we get:

`\begin{aligned} g(x) &= x^2 + 2\cdot 3 \cdot x + 6^2 \\\\ &= (x + h)^2 \end{aligned}`

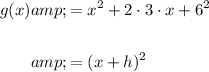
Thus, we can see that g(x) is a translation of f(x) to the right by h=6 units.

Note that we can also think of this translation as a shift to the left by -6 units. However, it is more common to describe translations in terms of positive shifts.