Question

In circle X, XY = 6 and the area of shaded sector = 15pi Find m/YXZ

Answer 1

m ∠ YXZ = 150°

Explanation:

Given:

• Area of sector = 15π
• XY (r) = 6

To find:

• m ∠ YXZ

Solution:

The area of a sector is given by the formula:

`\sf \textsf{Area of sector }= (\theta )/(360^\circ) \cdot \pi \cdot r^2`

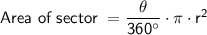
where θ is the central angle of the sector in degrees and r is the radius of the circle.

Substitute the known value and simplify.

`\sf 15\pi = (\theta )/(360^\circ) \cdot \pi \cdot 6^2`

`\sf 15 \cancel{\pi }= \frac{\theta }{\cancel{360^\circ}\cdot 10^\circ } \cdot \cancel{ \pi } \cdot \cancel{36 }`

`\sf 15 = (\theta )/(10^\circ)`

`\sf \theta = 15 \cdot 10^\circ`

`\sf \theta = 150^\circ`

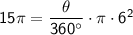
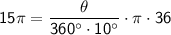
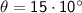
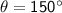
Therefore, the measure of m ∠ YXZ is 150°.