Answer:
Width = 6 miles; length = 10 miles
Explanation:
We can determine the dimensions of the plot of land using a system of equations, where:
- L represents its length,
- and W represents its width.
First equation:
Since the plot's length is 4 miles greater than its width, our first equation is given by:
L = W + 4
Second equation:
Since the formula for the area of a rectangle is given by A = LW (i.e., area = length * width) and the area of the plot is 60 square miles, our second equation is given by:
60 = LW
Method to solve: Substitution:
Solving for W:
We can solve for W by substituting W + 4 for L in 60 = LW (i.e., the second equation:)
60 = (W + 4)(W)
60 = W^2 + 4W
Rewrite the equation in the standard form of a quadratic (i.e., ax^2 + bx + c = 0):
Now, we can arrange the equation to be in the standard form of a quadratic:
(60 = W^2 + 4W) - W^2 - 4W
-W^2 - 4W + 60 = 0
Note that -W^2 is the same as -1W^2, meaning we can write our equation as:
-1W^2 - 4W + 60 = 0
Solving the quadratic with the quadratic formula:
The quadratic formula is given by:
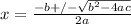, where:
- x represent the solution(s) to the quadratic,
- and a, b, and c are numbers from the standard form.
Thus, we can solve the quadratic by substituting -1, -4, and 60 for a, b, and c in the quadratic formula:
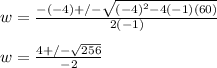
Now, we can begin splitting up the quadratic to find the positive solution and the negative solution:
Positive solution:
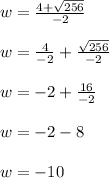
- Therefore, the positive solution is -10. Since width can't be negative, we can eliminate this answer, meaning that the width will be our negative solution.
Negative solution:
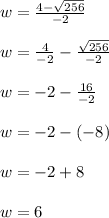
Therefore, the width of the plot is 6 miles.
Solving for L:
Now, we can solve for L by plugging in 6 for W in L = W + 4:
L = 6 + 4
L = 10
Therefore, the length of the plot is 10 miles.