Question

A line passes through the points (

–
5,5) and (7,
–
5). Write its equation in slope-intercept form

Answer 1

`\boxed{\boxed{\sf y = -(5)/(6)x + (5)/(6)}}`

Explanation:

Let the given coordinates be (-5,5) and (7,-6)

To find the equation of the line in slope-intercept form, we first need to find the slope of the line.

The slope of a line is calculated as follows:

`\sf slope = (y_2 - y_1)/(x_2 - x_1)`

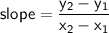
Where (x1, y1) and (x2, y2) are two points on the line.

In this case, we have the points (-5, 5) and (7, -5).

Substituting these values into the slope formula, we get:

`\sf slope = (-5 - 5)/(7 - (-5)) \\\\ = (-10)/(12) \\\\ =-(5)/(6)`

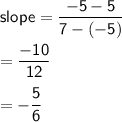
Now that we know the slope of the line, we can find the y-intercept by using one of the two points on the line. Let's use the point (-5, 5).

`\boxed{\sf y = mx + b }`

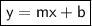
Substituting the slope and the point into the equation, we get:

`\sf 5 = - (5)/(6)(-5) + b`

`\sf b =5 - (25)/(6)`

`\sf b = (6\cdot 5 - 25)/(6)`

`\sf b = (5)/(6)`

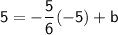
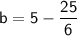
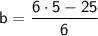
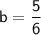
Therefore, the equation of the line in slope-intercept form is:

`\boxed{\boxed{\sf y = -(5)/(6)x + (5)/(6)}}`