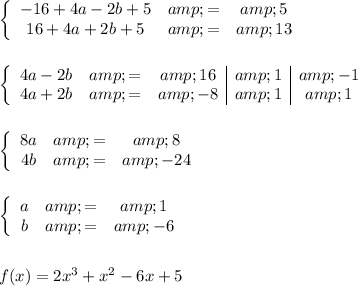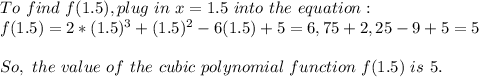Question

a cubic polynomial function f has leading coefficient of 2 and a constant term of 5. when f(-2)=5 and f(2)=13, what is f(1.5)

Answer 1

Hi,

Explanation:

To find the value of the cubic polynomial function f(1.5) given that f has a leading coefficient of 2 and a constant term of 5, and that f(-2) = 5 and f(2) = 13, we can write the general form of the cubic polynomial as:

`f(x) = 2x^3 + ax^2 + bx + 5`

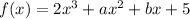
Now we can use the information that f(-2) = 5 and f(2) = 13 to set up two equations:

`f(-2) = 2(-2)^3 + a(-2)^2 + b(-2) + 5 = 5\\f(2) = 2(2)^3 + a(2)^2 + b(2) + 5 = 13\\`

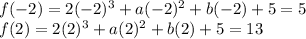
Simplify these equations:

`\left\{\begin{array}{ccc}-16 + 4a - 2b + 5 &=& 5\\16 + 4a + 2b + 5 &=& 13\\\end {array} \right.\\\\\\\left\{\begin{array}c4a - 2b &=& 16&1&-1\\4a + 2b &=& -8&1&1\\\end {array} \right.\\\\\\\left\{\begin{array}{ccc}8a &=& 8\\4b &=& -24\\\end {array} \right.\\\\\\\left\{\begin{array}{ccc}a &=& 1\\b &=& -6\\\end {array} \right.\\\\\\f(x)=2x^3+x^2-6x+5\\`

`To\ find\ f(1.5), plug\ in\ x = 1.5\ into\ the\ equation:\\f(1.5) = 2*(1.5)^3 + (1.5)^2 - 6(1.5) + 5=6,75+2,25-9+5=5\\\\So,\ the\ value\ of\ the\ cubic\ polynomial\ function\ f(1.5)\ is\ 5.`