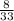Step-by-step explanation
In the question, we are given that;

Since each of the vehicles is equally likely to leave;
Part A
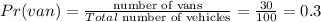
Answer: 0.3
Part B
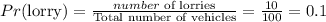
Answer: 0.1
Part C
First we find the probability of a lorry or van leaving

Next, we find the probability of a car; but remember that one of either a lorry or van has left the car park already, so the total number of vehicles will reduce by 1
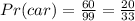
Therefore, the probability of a car leaving second if either a lorry or van had left first is
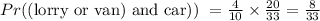
Answer: