Answer:
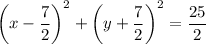
Explanation:
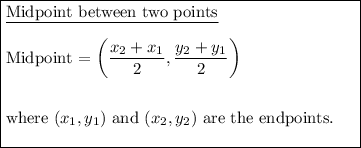
Given endpoints of the diameter of the circle:
- (x₁, y₁) = A (7, -3)
- (x₂, y₂) = B (0, -4)
To find the center of the circle, substitute the given endpoints into the midpoint formula:
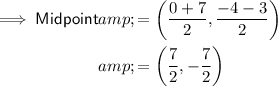

Substitute the found center and one of the given points (0, -4) into the equation and solve for r²:
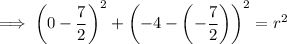
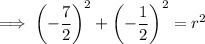

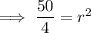
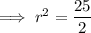
Therefore, the equation of the circle is:
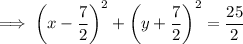
The graph of the circle is attached.