Question

I NEED HELP ASAP PLEASE 50 POINTS!!!

Answer 1

Answer: 71

Explanation:

Since triangles HJG and YZX are congruent and isosceles angles G and J are the same. Using CPCTC we can say that angles H and Y are the same. The sum of all angles in a triangle is 180 so 38+2x=180, x=71

Answer 2

∠G = 71°

∠J = 71°

Explanation:

Given:

∆ HJG ≅ ∆ YZX

∆ HJG is isoceles triangles.

So,

∠G = ∠J

Since the corresponding sides and angles of congruent triangles are equal

Let's take a look at angles only:

∠G = ∠X

∠H = ∠Y = 38°

∠J = ∠Z

Since the interior angles of a triangle is 180°

So,

∠G + ∠X + ∠H = 180°

Substitute the known value:

∠G + ∠X + 38° = 180°

Since ∠G = ∠X. So,

∠G + ∠G + 38° = 180°

2∠G + 38° = 180°

Subtract 38° on both sides:

2∠G + 38° - 38° = 180° - 38°

2∠G = 142°

Divide both sides by 2.

`\sf \angle G =(142^\circ)/(2)`

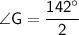
∠G = 71°

and

∠J = 71°

Therefore, the value of ∠G and ∠J is 71° for both.