Question

An A.P. has 20 terms and a common dif ference of 3. Determine the last term and the first term of the A.P. if its sum is (a) 165 (b) 650​

Answer 1

a)

• 1st term: - 20.25
• last term: 36.75

b)

• 1st term: 4
• last term: 61

Explanation:

Part (a)

Let a be the first term and l be the last term of the A.P.

We know that the sum of an A.P. is given by the formula:

`\sf S_n = (n)/(2) \left(2a + (n - 1)d\right)`

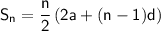
where n is the number of terms in the A.P. and d is the common difference.

In this case, we have n = 20, d = 3, and Sn = 165. We can now plug these values into the formula to solve for a and l:

`\sf 165 = (20)/(2) (2a + (20 - 1)3)`

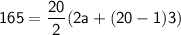
165 = 10(2a + 57)

`\sf 165 = 20a + 570`

`\sf 165 - 570 = 20a`

`\sf 20a = -405`

`\sf a =(-405)/(20)`

`\sf a = -20.25`

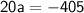
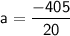
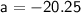
To find the last term, we can use the formula for the nth term of an A.P.:

`\sf a_n = a + (n - 1)d`

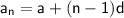
Plugging in a = -20.25, n = 20, and d = 3, we get:

l = -20.25 + (20 - 1)3

l = -20.25 + 57

l = 36.75

Therefore, the first term of the A.P. is -20.25 and the last term is 36.75.

Part (b)

Using the same approach as in part (a), we can solve for a and l:

`\sf 650 =( 20)/(2)(2a + (20 - 1)3)`

`\sf 650 = 10(2a + 57)`

`\sf 650 = 20a + 570`

`\sf 650 - 570= 20a`

`\sf 20a = 80`

`\sf a =(80)/(20)`

`\sf a = 4`

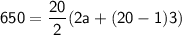
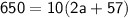
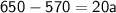
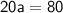
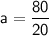
To find the last term, we can use the formula for the n th term of an A.P.:

`\sf a_n = a + (n - 1)d`

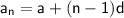
Plugging in a = 4, n = 20, and d = 3, we get:

l = 4 + (20 - 1)3

l = 4 + 57

l = 61

Therefore, the first term of the A.P. is 4 and the last term is 61.