Question

1/tana - 1/tan2a =cosec2a prove it ​

Answer 1

See below

Explanation:

To prove that
`\sf (1)/(\tan ( a )) -( 1)/(tan(2a)) =cosec(2a)` , we can start by expanding the left-hand side of the equation:

`\sf (1)/(\tan ( a )) -( 1)/(tan(2a)) = (\cos ( a ))/(\sin ( a )) - (\cos ( 2a ))/(\sin(2a))`

Using
`\boxed{\sf tan(\theta) =(sin\theta)/(cos\theta)}`

We can then use the identity
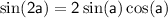`\sf \sin(2a) = 2\sin(a)\cos(a)` to simplify the equation:

`\sf = (\cos ( a ))/(\sin ( a )) - (\cos ( 2a ))/( 2\sin(a)\cos(a))`

Taking L.C.M and simplifying it.

`\sf = ( \cos(a) \cdot 2\cos(a) - \cos(2a) )/(2\sin(a)\cos(a))`

`\sf =( 2 \cos^2(a) - (cos^2(a) - sin^2(a) ) )/( 2\sin(a)\cos(a))`

`\sf = ( cos^2(a) + sin^2 (a) )/(2\sin(a)\cos(a))`

Using Pythagorean identity
`\sf cos^2(a) + \sin^2(a) = 1`

`\sf =(1)/(2\sin(a)\cos(a))`

Again using identity property
`\sf \sin(2a) = 2\sin(a)\cos(a)`

`\sf =(1)/(sin(2a))`

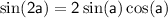
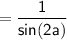
Using
`\sf sin \theta =(1)/(cosec \theta )`

`\sf =cosec (2a)`

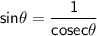
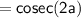
Since it is Right hand side.

Hence proved.